Spencer Quiel is an Assistant Professor in the Department of Civil and Environmental Engineering at Lehigh University.  His research focuses on resistance to extreme loads. 

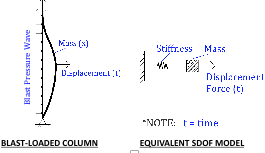
In recent years, blast hazards due to acts terrorism have resulted in significant damage to several structures, including the Murrah Federal Building in Oklahoma City in 1995 and the Khobar Towers in 1996.  Accidental blasts, such as a 2011 gas utility explosion in Allentown, PA, have also caused significant damage to neighboring buildings and other infrastructure. Though relatively infrequent, blast hazards can cause extensive amounts of property damage and, more importantly, loss of human life. The design of structures to resist the effects of blast due to an explosive detonation is performed using a variety of analysis tools to simulate dynamic structural response to a blast-induced shock wave.  The most common method in the current state-of-practice is the Single-Degree-of-Freedom (SDOF) method, which has also been used to model structural response to other dynamic loading such as earthquake-induced vibration.  An SDOF system is a mathematical model in which a structural element is collectively represented as a single mass, spring, and damper to which a force time history is applied.  A representative SDOF model for a blast-loaded column is shown below.

For blast threats at large standoff distances, previous experimental and computational studies have shown that the static bending shape assumption used by SDOF analysis is reasonable.  However, experimental data and advanced analysis tools have shown that the SDOF method has difficulty in accurately capturing blast effects that are close range but not close enough to cause breach (or “punching”) damage.  These “intermediate” range blast threats constitute a significant portion of the design-basis threats that are considered in current practice, and therefore the applicability of SDOF analysis for these cases is of great interest to the industry.

Continue reading Limits of Single-Degree-of-Freedom Analysis of Structural Response to Blast →

Paolo Bocchini is a an Assistant Professor of Structural Engineering at Lehigh University and Javier Buceta is an Associate Professor of Chemical Engineering at Lehigh University. Their research synergy, together with Graziano Fiorillo, a Postdocoral Research Associate in Dr. Bocchini’s and Dr. Buceta’s labs, led them to begin developing models for predicting ebola outbreaks.  

What is the chance that two structural engineers and a physicist team up to fight one of the deadliest diseases in the history of humankind? Well, it looks like the plot of a Dan Brown novel, but it really happened, and it all started literally by “chance”, probability.

In 2014 a group of us, Lehigh University faculty, noticed that our university has a high density of researchers interested in Probabilistic Modeling and its applications to engineering and science, spread across various departments and colleges. For this reason, we decided to start coordinating our graduate courses to create a better synergy. But you know how it works: if you put two or more professors in the same room, they start talking about their research. So, at some point, Javier described his innovative way to model the non-homogeneous migration of bats infected by Ebola, which seems to be the main mechanism in which the virus travels for hundreds of miles triggering outbreaks in cities that did not see it coming and are completely unprepared for it, with devastating effects. Then Paolo noticed that the mathematical formulation and the type of uncertainties in the model that Javier used for infected bat migration have strong similarities with the way in which he addresses the uncertain propagation of seismic waves over a large region. It was (scientific) love at first sight. Paolo and Javier immediately saw the potential of combining Paolo’s novel hazard models and the rigorous framework that civil engineers use for catastrophe modeling, with the cutting-edge technique that Javier was developing to capture the disease spreading. The outcome is a comprehensive tool that can predict (in a probabilistic sense) the risk of Ebola outbreaks over a region as broad as the entire African continent and, in this way, drive preemptive allocation of limited resources in the most effective way, to fight promptly outbreaks if they happen to occur.

With this idea, we (Paolo and Javier) submitted a Collaborative Research (CORE) proposal that was funded (thank you Lehigh!) and allowed us to hire a postdoc and bootstrap this new line of research. As you may imagine, it wasn’t easy to find a person with the right competences and enough curiosity to join us in this adventure at the boundary of several disciplines. Luckily, we found Graziano, who with his expertise in probabilistic modeling applied to engineering problems and his proficiency with high-performance computing has been the perfect scholar to carry on this project. With enthusiasm, our “bold trio” started working against Ebola in early 2016 (some people make fun of us saying that we are rather a “bald trio”).

Continue reading Probability, differential equations, and catastrophe models united against Ebola →